Figure 11.6

[ASKurz]

In Section 11.1.5, With intention to make multiple tests, Kruschke presented an NHST simulation. From the text, we read:

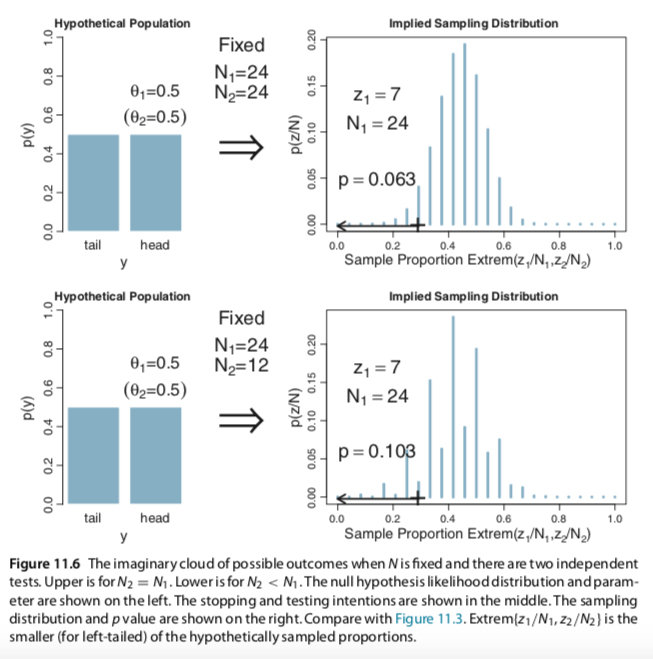
Suppose that we want to test the hypothesis of fairness for a coin, and we have a second coin in the same experiment that we are also testing for fairness. In real biological research, for example, this might correspond to testing whether the male/female ratio of babies differs from 50/50 in each of two species of animal. We want to monitor the false alarm rate overall, so we have to consider the probability of a false alarm from either coin. Thus, the p value for the first coin is the probability that a proportion, equal to or more extreme than its actual proportion, could arise by chance from either coin....

For concreteness, suppose we flip both coins N1 = N2 = 24 times, and the first coin comes up heads z1 = 7 times. This is the same result as in the previous examples. Suppose that we intended to stop when the number of flips reached those limits. The p value for the outcome of the first coin is the probability that either z1/N1 or z2/N2 would be as extreme, or more extreme, than 7/24 when the null hypothesis is true. This probability will be larger than when considering a single coin, because even if the imaginary flips of the first coin do not exceed 7/24, there is still a chance that the imaginary flips of the second coin will. For every imaginary sample of flips from the two coins, we need to consider the sample proportion, either z1/N1 or z2/N2, that is most extreme relative to θ. The p value is the probability that the extreme proportion meets or exceeds the actual proportion.

Figure 11.6 shows the numerical details for this situation. The upper-right panel shows the sampling distribution of the extreme of z1/N1 or z2/N2, when the null hypothesis is true and the stopping intention is fixed N for both coins. You can see that the p value for z1/N1 = 7/24 is p = 0.063. (pp. 310--311)

Here's a copy of Figure 11.6:

If you have the chops to reproduce this simulation and plot, please share your code. If at all possible tidyverse-oriented workflows are preferred.