Skip to content

Latest commit

 

History

History
499 lines (368 loc) · 33 KB

Dimension Reduction.md

File metadata and controls

499 lines (368 loc) · 33 KB

Dimension Reduction and Manifold Learning

Principal component analysis or singular value decomposition can be applied to matrix approximation. The data collected in practice always save in the table form, which can considered as a matrix. Another techniques similar to PCA is eigenvalue-eigenvector decomposition. Dimension reduction is really the topic of data science as data preprocessing .

The basic idea of dimension reduction is that not all information is necessary for a specific task. The motivation of dimension reduction is Curse of Dimensionality, limit of storage/computation and so on. The high dimensional space is not easy for us to visualize, imagine or understand. The intuition or insight to high dimensional space is weak for us, the people who live in the three dimensional space. As a preprocessing data method, it helps us to select features and learn proper representation.
The dimension reduction is related with geometry of data set, which includes manifold learning and topological data analysis.

All manifold learning algorithms assume that data set lies on a smooth non-linear manifold of low dimension and a mapping

$$ f:\mathbb{R}^D\to\mathbb{R}^d $$

(where $D\gg d$) can be found by preserving one or more properties of the higher dimension space. For example, dimension reduction seems to be quasi-isometric: $$ |f(x)|\approx | x|, |f(x) -f(y)|\approx | x - y|. $$

$\color{aqua}{PS:}$ the dimension reduction is classified into unsupervised learning while it can be converted to optimization problems. Additionally, it will miss some properties of the data set so please do not delete the previous data sets.

What is more, the blessings of dimensionality include the concentration of measure phenomenon (so-called in the geometry of Banach spaces), which means that certain random fluctuations are very well controlled in high dimensions and the success of asymptotic methods, used widely in mathematical statistics and statistical physics, which suggest that statements about very high-dimensional settings may be made where moderate dimensions would be too complicated.

It is a wonderful review of dimension reduction at TiCC TR 2009–005, Dimensionality Reduction: A Comparative Review, Laurens van der Maaten Eric Postma, Jaap van den Herik TiCC, Tilburg University.

A related top is data compression, a branch of information theory, a more useful and fundamental topic in computer science.

PCA and MDS

The data in table form can be regarded as matrix in mathematics. And we can apply singular value decomposition to low rank approximation or non-negative matrix factorization, which we will talk in PCA and SVD. It is classified as linear techniques. And it can extend to kernel PCA and generalized PCA.

Multi-Dimension Scaling is a distance-preserving manifold learning method. Distance preserving methods assume that a manifold can be defined by the pairwise distances of its points. In distance preserving methods, a low dimensional embedding is obtained from the higher dimension in such a way that pairwise distances between the points remain same. Some distance preserving methods preserve spatial distances (MDS) while some preserve graph distances.

MDS is not a single method but a family of methods. MDS takes a dissimilarity or distance matrix ${D}$ where $D_{ij}$ represents the dissimilarity between points ${i}$ and ${j}$ and produces a mapping on a lower dimension, preserving the dissimilarities as closely as possible. The dissimilarity matrix could be observed or calculated from the given data set. MDS has been widely popular and developed in the field of human sciences like sociology, anthropology and especially in psychometrics. From blog.paperspace.com.

It is a linear map $$ {X}\in\mathbb{R}^D\to {Z}\in\mathbb{R}^d\ Z = W^T X $$

Steps of a Classical MDS algorithm:

Classical MDS uses the fact that the coordinate matrix can be derived by eigenvalue decomposition from ${\textstyle B= Z Z^T}$. And the matrix ${\textstyle B}$ can be computed from proximity matrix ${\textstyle D}$ by using double centering.

  • Set up the squared proximity matrix ${\textstyle D^{(2)}=[d_{ij}^{2}]}$
  • Apply double centering: $B=-{\frac{1}{2}J D^{(2)}J}$ using the centering matrix ${\textstyle J=I-{\frac {1}{n}11'}}$, where ${\textstyle n}$ is the number of objects.
  • Determine the ${\textstyle m}$ largest eigenvalues $\lambda_{1},\lambda_{2},...,\lambda_{m}$ and corresponding eigenvectors ${\textstyle e_{1},e_{2},...,e_{m}}$ of ${\textstyle B}$ (where ${\textstyle m}$ is the number of dimensions desired for the output).
  • Now, ${\textstyle Z=E_{m}\Lambda_{m}^{1/2}}$ , where ${\textstyle E_{m}}$ is the matrix of ${\textstyle m}$ eigenvectors and ${\textstyle \Lambda_{m}}$ is the diagonal matrix of ${\textstyle m}$ eigenvalues of ${\textstyle B}$.

Classical MDS assumes Euclidean distances. So this is not applicable for direct dissimilarity ratings.

Locally Linear Embedding

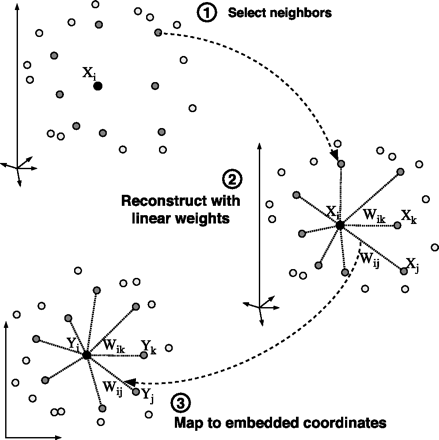
Locally Linear Embedding(LLE) is a topology preserving manifold learning method. Topology preservation means the neighborhood structure is intact. Methods like SOM(self-organizing map) are also topology preserving but they assume a predefined lattice for the lower manifold. LLE creates the lattice based on the information contained in the dataset.

  1. Compute the neighbors of each data point, $\vec{X}_i$.
  2. Compute the weights $W_{ij}$ that best reconstruct each data point $\vec{x_i}$ from its neighbors, minimizing the cost $\sum_{i}|\vec{X}i - \sum{j}W_{ij}\vec{X}_j|^2$ by constrained linear fits.
  3. Compute the vectors $\vec{Y}i$ best reconstructed by the weights $W{ij}$, minimizing the quadratic form $\sum_{i}|\vec{Y}i - \sum{j}W_{ij}\vec{Y}_j|^2$ by its bottom nonzero eigenvectors.

Auto-Encoder

Auto-Encoder is a neural network model that compresses the original data and then encodes the compressed information such as $$\mathbb{R}^{p}\stackrel{\sigma}{\to}\mathbb{R}^{n}\stackrel{\sigma}{\to}\mathbb{R}^{d}$$ where $n\le d=p$ and $\sigma$ is nonlinear activation function. We can express it in mathematical formula $$ y=\sigma(x)\in\mathbb{R}^{n},z=\sigma(y)\in\mathbb{R}^{d}, $$ where $x$, $y$, $z$ is the input, the hidden unit and output, respectively. It is trying to learn an approximation to the identity function, so as to output $z$ that is similar to $x$.

Now suppose we have only unlabeled training examples set ${x^{(1)}, x^{(2)}, x^{(3)}, \dots}$, where $x^{(i)}\in\mathbb{R}^{p}$.

An auto-encoder neural network is an unsupervised learning algorithm that applies back-propagation, setting the target values to be equal to the inputs. I.e., it uses $z^{(i)} = x^{(i)}$. It is trying to learn an approximation to the identity function, so as to output $\hat{x}$ that is similar to $x$. The identity function seems a particularly trivial function to be trying to learn; but by placing constraints on the network, such as by limiting the number of hidden units, we can discover interesting structure about the data.

Recall that $y^{(j)}$ denotes the activation of hidden unit $j$ in the auto-encoder and write $y^{(j)}(x)$ to denote the activation of this hidden unit when the network is given a specific input $x$, i.e., $y^{(j)}(x)=\sigma\circ(x)^{(j)}$. Let $\hat{\rho}j=\frac{1}{m}\sum{i=1}^{m}y^{j}(x^{(i)})$ be the average activation of hidden unit $j$ (averaged over the training set). We will add an extra penalty term to our optimization objective that penalizes $\rho^j$ deviating significantly from $\rho$. We will choose the following:

$$ \sum_{j=1}^{n}\rho\log(\frac{\rho}{\hat{\rho}^j})+(1-\rho)\log(\frac{1-\rho}{1-\hat{\rho}^j}). $$

And we will minimize the objective function

$$ \sum_{i=1}^{m}L(x^{(i)},z^{(i)})+[\rho\log(\frac{\rho}{\hat{\rho}^j})+(1-\rho)\log(\frac{1-\rho}{1-\hat{\rho}^j})] $$

via backpropagation, where $L(\cdot , \cdot)$ is a loss function and $z^{(i)}$ is the output of sparse autoencoder when the input is $x^{(i)}$.

If we want to compress the information of the data set, we only need output of hidden units $y^{(i)}=\sigma\circ(x^{(i)})$, which maps the data in higher dimensional space to a low dimensional space $$ \mathbb{R}^{p}\to\mathbb{R}^{n}\ x\to \sigma\circ(W_1 x+b_1). $$ Given an compressed data ${y^{(i)}}$ via a autoencoder, we can decode it by the output layer $z^{(i)}=\sigma\circ(W_2 y^{(i)} + b_2)$.

t-SNE

The basic idea of t-SNE is that the similarity should preserve after dimension reduction. It maps the data $x$ in high dimensional space $X\subset\mathbb{R}^{p}$ to a low dimensional space $Y\subset\mathbb{R}^{d}$. t-SNE is an extension of stochastic neighbor embedding.

Stochastic Neighbor Embedding (SNE) starts by converting the high-dimensional Euclidean distances between data points into conditional probabilities that represent similarities. The similarity of data point $x_j$ to data point $x_i$ is the conditional probability, $p_{j|i}$, that $x_i$ would pick $x_j$ as its neighbor if neighbors were picked in proportion to their probability density under a Gaussian centered at $x_i$. Mathematically, the conditional probability $p_{j|i}$ is given by $$ p_{j|i} = \frac{exp(-|x_i-x_j|^2/2\sigma_i^2)}{\sum_{k\ne 1} exp(-|x_k-x_i|^2/2\sigma_i^2)}. $$

Because we are only interested in modeling pairwise similarities, we set the value of $p_{i|i}$ to zero. For the low-dimensional counterparts $y_i$ and $y_j$ of the high-dimensional data points $x_i$ and $x_j$, it is possible to compute a similar conditional probability, which we denote by $q_{j|i}$. we model the similarity of map point $y_j$ to map point $y_i$ by $$q_{j|i}=\frac{exp(-|y_i-y_j|^2)}{\sum_{k\ne i}exp(-|y_k-y_i|^2)}.$$

SNE minimizes the sum of cross entropy over all data points using a gradient descent method. The cost function $C$ is given by $$C=\sum_{i}\sum_{j}p_{j|i}\log(\frac{p_{j|i}}{q_{j|i}}).$$

In the high-dimensional space, we convert distances into probabilities using a Gaussian distribution. In the low-dimensional map, we can use a probability distribution that has much heavier tails than a Gaussian to convert distances into probabilities. In t-SNE, we employ a Student t-distribution with one degree of freedom (which is the same as a Cauchy distribution) as the heavy-tailed distribution in the low-dimensional map. Using this distribution, the joint probabilities $q_{i|j}$ are defined as $$ q_{i|j} = \frac{(1+|y_i-y_j|^2)^{-1}}{\sum_{j\not= i} (1+|y_i - y_j|^2)^{-1}}. $$

ICA

Independent component analysis is to find the latent independent factors that make up the observation, i.e, $$ x_j = b_{j1}s_1 + b_{j2}s_2 + \dots + b_{jn} s_n,\forall j\in{1,2,\dots,n} \ x=Bs $$

where $x$, $s$, $B$ is the observation, latent variable and unknown mixing matrix. The ICA model is a generative model, which means that it describes how the observed data are generated by a process of mixing the components $s_i$. The independent components are latent variables, meaning that they cannot be directly observed. Also the mixing matrix $B$ is assumed to be unknown. All we observe is the random vector ${x}$, and we must estimate both ${B}$ and ${s}$ using it. This must be done under as general assumptions as possible.

In the ICA model, we assume that each mixture $x_j$ as well as each independent component $s_k$ is a random variable. Without loss of generality, we can assume that both the mixture variables and the independent components have zero mean.

Different from the principal components in PCA, the independent components are not required to be perpendicular to each other.

The starting point for ICA is the very simple assumption that the components $s_i$ are statistically independent. The fundamental restriction in ICA is that the independent components must be nongaussian for ICA to be possible. And if the mixing matrix ${B}$ is inversible so that $W=B^{-1}$ and $s=Wx$.

In order to solve $x=Bs$, we assume that each independent component $s_i$ has unit variance: $\mathbb{E}(s_i^2)=1$. The independence of random variables is not obvious when we do not know their probability distribution. Since independence implies uncorrelatedness, many ICA methods constrain the estimation procedure so that it always gives uncorrelated estimates of the independent components. This reduces the number of free parameters, and simplifies the problem.

Intuitively speaking, the key to estimating the ICA model is nongaussianity. Actually, without nongaussianity the estimation is not possible at all.

The classical measure of nongaussianity is kurtosis or the fourth-order cumulant. The kurtosis of random variable ${y}$ is classically defined by $$kurt(y)=\mathbb{E}(y^4)-3{\mathbb{E}(y^2)}^2.$$ A second very important measure of nongaussianity is given by negentropy ${J}$, which is defined as $$J=H(y_{gauss})-H(y)$$ where $y_{gauss}$ is a Gaussian random variable of the same covariance matrix as ${y}$ and $H(\cdot)$ is the entropy function. Estimating negentropy using the definition would require an estimate (possibly nonparametric) of the pdf. Therefore, simpler approximations of negentropy are very useful such as $$J(y)\approx \frac{1}{12}{\mathbb{E}(y^3)}^2+\frac{1}{48}kurt(y)^2.$$ Denoting ${B}^{-1}$ by the matrix $W=(w_1,w_2,\dots,w_n)^T$ and $y=Wx$, the log-likelihood takes the form $$L=\sum_{t=1}^{T} \sum_{i=1}^{n}\log f_i(w_i^Tx(t))+T\log(|det(W)|)$$ where the $f_i$ are the density functions of the $s_i$ (here assumed to be known), and the $x(t),t = 1,...,T$ are the realizations of $x$. And we constrain the $y_i(t)=w_i^Tx(t)$ to be uncorrelated and of unit variance.

It is proved the surprising result that the principle of network entropy maximization, or “infomax”, is equivalent to maximum likelihood estimation.

ICA is very closely related to the method called blind source separation (BSS) or blind signal separation and see more on Blind Identification of Potentially Underdetermined Mixtures.

Exploratory Projection Pursuit

Projection pursuit is a classical exploratory data analysis method to detect interesting low-dimensional structures in multivariate data. Originally, projection pursuit was applied mostly to data of moderately low dimension. Peter J Huber said in Projection Pursuit:

The most exciting features of projection pursuit is that it is one of few multivariate methods able to bypass the "curse of dimensionality" caused by the fact that high-dimensional space is mostly empty.

PP methods have one serious drawback: their high demand on computer time.

Discussion by Friedman put that

Projection pursuit methods are by no means the only ones to be originally ignored for lack of theoretical justification. Factor analysis, clustering, multidimensional scaling, recursive partitioning, correspondence analysis, soft modeling (partial-least-squares), represent methods that were in common sense for many years before their theoretical underpinnings were well understood. Again, the principal justification for their use was that they made sense heuristically and seemed to work well in a wide variety of situations.

It reduces the data of dimension ${m}$ to dimension ${p}$ for visual inspection. This method consists of defining a measure of information content in two dimension and optimizing that measure or index as a function of two m-dimensional projection vectors to find the most informative projection.

The minimal ingredients of an EPP algorithm are then as follows:

  • (1) choose a subspace of the desired dimension and project the data onto the subspace,
  • (2) compute some index of 'information content' for the projection,
  • and (3) iterate 1 and 2 until the index is maximized.

In more mathematical language, EPP involves choosing some dimension ${p}$ for the projection subspace, defining an index of interestingness for random variables in dimension ${p}$, say $f(X(\alpha), \alpha)$, and devising some method to optimize ${f}$ over all possible projection unit vectors $\alpha, |\alpha|=1$. Note that in a subspace, the random variable is always directly dependent upon the projection given by ${\alpha}$ but for convenience the notation is sometimes suppressed.

Assume that the $p$ -dimensional random variable $X$ is sphered and centered, that is, $E(X)=0$ and $Var(X) = {\cal{I}}_p$. This will remove the effect of location, scale, and correlation structure.

Friedman and Tukey (1974) proposed to investigate the high-dimensional distribution of ${X}$ by considering the index

$$ \frac{1}{n}\sum_{i=1}^{n}\hat{f} (\left<\alpha, X_i\right>) $$

and $\hat{f}(z) = \frac{1}{n}\sum_{j=1}^{n} K (z -\left&lt;\alpha, X_j\right&gt;)$ with some kernel function ${K}$. If the high-dimensional distribution of $X$ is normal, then each projection $z=\alpha^{\top}X$ is standard normal since $\vert\vert\alpha\vert\vert=1$ and since ${X}$ has been centered and sphered by, e.g., the Mahalanobis transformation.

The projection pursuit methods can extend to density estimation and regression.

Self Organizing Maps

One source of ICA is "general infomax learning principle" well known in machine learning or signal processing community.

However, we can not explain all efficient methods in mathematics or statistics then write it in the textbook. Self organizing map is not well-known. These networks are based on competitive learning; the output neurons of the network compete among themselves to be activated or fired, with the result that only one output neuron, or one neuron per group.

Each node has a specific topological position (an x, y coordinate in the lattice) and contains a vector of weights of the same dimension as the input vectors. That is to say, if the training data consists of vectors, $V$, of $n$ dimensions:

$$V_1, V_2, V_3, \cdots, V_n.$$

Then each node will contain a corresponding weight vector ${W}$, of ${n}$ dimensions:

$$W_1, W_2, W_3, \cdots, W_n.$$

Training occurs in several steps and over many iterations:

  • Each node's weights are initialized.
  • A vector is chosen at random from the set of training data and presented to the lattice.
  • Every node is examined to calculate which one's weights are most like the input vector. The winning node is commonly known as the Best Matching Unit (BMU).
  • The radius of the neighbourhood of the BMU is now calculated. This is a value that starts large, typically set to the 'radius' of the lattice,
    but diminishes each time-step. Any nodes found within this radius are deemed to be inside the BMU's neighbourhood.
  • Each neighbouring node's (the nodes found in step 4) weights are adjusted to make them more like the input vector. The closer a node is to the BMU, the more its weights get altered.
  • Repeat step 2 for N iterations.

Diffusion map

Diffusion map uses the eigen-vectors to define coordinate system.

https://www.wikiwand.com/en/Diffusion_map

Hessian Eigenmaps

Isomap

Laplacian Eigenmaps

Local Tangent Space Alignment

Uniform Manifold Approximation and Projection

Uniform Manifold Approximation and Projection (UMAP) is a dimension reduction technique that can be used for visualisation similarly to t-SNE, but also for general non-linear dimension reduction. The algorithm is founded on three assumptions about the data

  • The data is uniformly distributed on Riemannian manifold;
  • The Riemannian metric is locally constant (or can be approximated as such);
  • The manifold is locally connected.

From these assumptions it is possible to model the manifold with a fuzzy topological structure. The embedding is found by searching for a low dimensional projection of the data that has the closest possible equivalent fuzzy topological structure.

Intrinsic Dimension

In Description Of Intrinsic Dimension 2019, Yoav Freund pointed out that:

It is often the case that very high dimensional data, such as images, can be compressed into low dimensional vectors with small reconstruction error. The dimension of these vectors is the intrinsic dimension of the data. We will discuss several techniques for estimating intrinsic dimension and for mapping data vectors to their low-dimensional representations. The ultimate goal is to find streaming algorithms can can process very large dataset in linear or sub-linear time.

In mathematical terms, let the original data be given by the finite sequence of points $$\mathcal{X}={x_1,x_2,\cdots,x_N}$$ where $x_i\in\mathbb{R}^d$ for $i=1,2,\cdots, N$. In the model-driven approach, one assumes that there exists a sequence of generating variables of minimal dimension $m$ $$\mathcal{Y}={y_1, y_2,\cdots, y_N}$$ where $y_i\in\mathbb{R}^m$ for $i=1,2,\cdots, N$, and a mapping function $$f:\mathbb{R}^m\to\mathbb{R}^d, f(y_i)=x_i\qquad\forall\quad i.$$ While specific knowledge about $f$ can certainly be useful in the process of dimensionality reduction, it is not compulsory. Moreover, in most practical applications, also the dimension $m$ of the generating space $\mathbb{R}^m$ is unknown a priori. Depending on the current perspective, $m$ is referred to as the number of latent variables or as the intrinsic dimension of the data $X$.

Yet, numerous reduction methods do not compute a target embedding dimension but rather rely on an external input parameter. Consequently, the estimation of the intrinsic dimension of a given dataset is essential for the proper functioning of those methods.

Methods for identifying the dimension：

  • Haussdorff dimension, Doubling dimension, epsilon-cover

Lebesgue covering dimension, also called topological dimension or just covering dimension, is defined with respect to a given topological space $(\mathcal{Y}, \tau )$, that is a set of points $\mathcal{Y}$ together with a collection $\tau$ of subsets of $\mathcal{Y}$ called open sets. For any subset $S \subset \mathcal{Y}$, a covering of $S$ is defined as a family $\mathcal{C}$ of open sets whose union contains $S$. Now the Lebesgue covering dimension of $S \subset \mathcal{Y}$ is defined as the smallest integer $D_L$, such that every covering $\mathcal{C}$ of $S$ has a refinement $C^{\prime}$, for which each point of $S$ is contained in at most $D_L +1$ sets of $C^{\prime}$. If such an integer does not exist, the covering dimension is infinite.

Set $S \subset \mathbb{R}^d$ has doubling dimension $d_o$ if for any (Euclidean) ball $B$, the subset $S \cap B$ can be covered by 2$d_o$ balls of half the radius.

Simplex Volumes

One popular example is the relationship of volumes between the unit hypercube and its inscribed d-ball. It might seem surprising at first that the volume of the corresponding d-ball tends to zero very quickly.

Metric Learning

Deep Metric Learning

The goal is to capture similarity between embeddings, such that the projected distance of similar items in the embedding space is smaller than the dissimilar items. Compared to the standard distance metric learning, it uses deep neural networks to learn a nonlinear mapping to the embedding space. It helps with extreme classification settings with huge number classes, not many examples per class.

Siamese Networks

  • Left and right legs of the network have identical structures (siamese);
  • Weights are shared between the siamese networks during training;
  • Networks are optimized with a loss function, such as contrastive loss.

https://people.eecs.berkeley.edu/~efros/courses/AP06/