Skip to content

Latest commit

 

History

History
132 lines (108 loc) · 8.83 KB

QuickScorer.md

File metadata and controls

132 lines (108 loc) · 8.83 KB

QuickScorer

QuickScorer was designed by Lucchese, C., Nardini, F. M., Orlando, S., Perego, R., Tonellotto, N., and Venturini, R. with the support of Tiscali S.p.A.

It adopts a novel bitvector representation of the tree-based ranking model, and performs an interleaved traversal of the ensemble by means of simple logical bitwise operations. The performance of the proposed algorithm are unprecedented, due to its cache-aware approach, both in terms of data layout and access patterns, and to a control flow that entails very low branch mis-prediction rates.

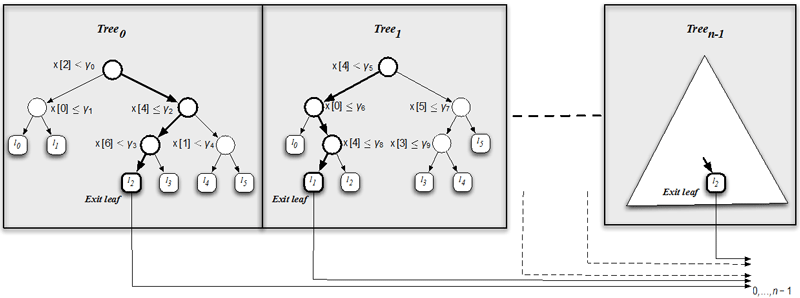
All the nodes whose Boolean conditions evaluate to False are called false nodes, and true nodes otherwise. The scoring of a document represented by a feature vector $\mathrm{x}$ requires the traversing of all the trees in the ensemble, starting at their root nodes. If a visited node in N is a false one, then the right branch is taken, and the left branch otherwise. The visit continues recursively until a leaf node is reached, where the value of the prediction is returned.

The building block of this approach is an alternative method for tree traversal based on bit-vector computations. Given a tree and a vector of document features, this traversal processes all its nodes and produces a bitvector which encodes the exit leaf for the given document.

Given an input feature vector $\mathrm x$ and a tree $T_h = (N_h;L_h)$, where $N_h$ is a set of internal nodes and $L_h$ is a set of leaves, our tree traversal algorithm processes the internal nodes of Th with the goal of identifying a set of candidate exit leaves, denoted by $C_h$ with $C_h \subset L_h$, which includes the actual exit leaf $e_h$. Initially $C_h$ contains all the leaves in $L_h$, i.e., $C_h = L_h$. Then, the algorithm evaluates one after the other in an arbitrary order the test conditions of all the internal nodes of $T_h$. Considering the result of the test for a certain internal node $n \in N_h$, the algorithm is able to infer that some leaves cannot be the exit leaf and, thus, it can safely remove them from $C_h$. Indeed, if $n$ is a false node (i.e., its test condition is false), the leaves in the left subtree of $n$ cannot be the exit leaf and they can be safely removed from $C_h$. Similarly, if $n$ is a true node, the leaves in the right subtree of n can be removed from $C_h$.

The second refinement implements the operations on $C_h$ with fast bit-wise operations. The idea is to represent $C_h$ with a bitvector ${\text{leaf_index}}_h$, where each bit corresponds to a distinct leaf in $L_h$, i.e., $\text{leaf_index}_h$ is the characteristic vector of $C_h$. Moreover, every internal node $n$ is associated with a bit mask of the same length encoding (with 0’s) the set of leaves to be removed from $C_h$ whenever $n$ turns to be a false node. In this way, the bitwise logical AND between $\text{leaf_index}_h$ and the bit mask of a false node $n$ corresponds to the removal of the leaves in the left subtree of $n$ from $C_h$. Once identified all the false nodes in a tree and performed the associated AND operations over $\text{leaf_index}_h$, the exit leaf of the tree corresponds to the leftmost bit set to 1 in $\text{leaf_index}_h$.

One important result is that Quick Scorer computes $s(x)$ by only identifying the branching nodes whose test evaluates to false, called false nodes. For each false node detected in $T_h \in T$ , Quick Scorer updates a bitvector associated with $T_h$, which stores information that is eventually exploited to identify the exit leaf of $T_h$ that contributes to the final score $s(x)$. To this end, Quick Scorer maintains for each tree $T_h \in T$ a bitvector leafidx[h], made of $\land$ bits, one per leaf. Initially, every bit in leafidx[h] is set to $\mathrm 1$. Moreover, each branching node is associated with a bitvector mask, still of $\land$ bits, identifying the set of unreachable leaves of $T_h$ in case the corresponding test evaluates to false. Whenever a false node is visited, the set of unreachable leaves leafidx[h] is updated through a logical $AND (\land)$ with mask. Eventually, the leftmost bit set in leafidx[h] identifies the leaf corresponding to the score contribution of $T_h$, stored in the lookup table leafvalues.

ALGORITHM 1: Scoring a feature vector $x$ using a binary decision tree $T_h$

  • Input:
    • $x$: input feature vector
    • $T_h = (N_h, L_h)$: binary decision tree, with
      • $N_h = {n_0, n_1, \cdots}$: internal nodes of $T_h$
      • $L_h = {l_0, l_1, \cdots}$: leaves of $T_h$
      • $n.mask$: node bit mask associated with $n\in N_h$
      • $l_j.val$: score contribution associated with leaf $l_j\in L_h$
  • Output:
    • tree traversal output value
  • $score(x, T_h)$:
    • $\text{leaf_index}_h\leftarrow (1,1,\dots, 1)$
    • $U\leftarrow FindFalse(x, T_h)$
    • foreach node $n \in U$ do
      • $\text{leaf_index}_h\leftarrow \text{leaf_index}_h\land n.mask$
    • $j \leftarrow\text{index of leftmost bit set to 1 of leaf_index}_h$
    • return $l_j.val$

ALGORITHM 2: : The QUICKSCORER Algorithm

  • Input:
    • $x$: input feature vector
    • $\mathcal T$: ensemble of binary decision trees, with
      • ${w_0, w_1, \cdots, w_{|\mathcal{T}|-1}}$: weights, one per tree
      • $thresholds$: sorted sublists of thresholds, one sublist per feature
      • $treeids$: tree’s ids, one per node/threshold
      • $nodemasks$: node bit masks, one per node/threshold
      • $offsets$: offsets of the blocks of triples
      • $leafindexes$: result bitvectors, one per each tree
      • $leafvalues$: score contributions, one per each tree leaf
  • Output:
    • final score of $x$
  • $\text{QUICKSCORER}(x, T_h)$:
    • foreach node $h \in {0,1\cdots, |T|-1}$ do
      • $\text{leaf_index}_h\leftarrow (1,1,\dots, 1)$
    • foreach node $k \in {0,1\cdots, |\mathcal{F}|-1}$ do
      • $i\leftarrow offsets[k]$
      • $end\leftarrow offsetsets[k+1]$
      • while $x[k] > thresholds[i]$ do
        • $h \leftarrow treeids[i]$
        • $\text { leafindexes }[h] \leftarrow \text { leafindexes }[h] \wedge \text { nodemasks }[i]$
        • $i\leftarrow i+1$
        • if $i\geq end$ then
          • break
    • $score \leftarrow 0$
    • foreach node $h \in {0,1\cdots, |T|-1}$ do
      • $j \leftarrow \text { index of leftmost bit set to 1 of},, {leafindexes }[h]$
      • $l \leftarrow h \cdot| L_{h} |+j$
      • $\text { score } \leftarrow \text { score }+w_{h} \cdot \text { leafvalues }[l]$
    • return $score$

vQS

Considering that in most application scenarios the same tree-based model is applied to a multitude of items, we recently introduced further optimisations in QS. In particular, we introduced vQS [3], a parallelised version of QS that exploits the SIMD capabilities of mainstream CPUs to score multiple items in parallel. Streaming SIMD Extensions (SSE) and Advanced Vector Extensions (AVX) are sets of instructions exploiting wide registers of 128 and 256 bits that allow parallel operations to be performed on simple data types. Using SSE and AVX, vQS can process up to eight items in parallel, resulting in a further performance improvement up to a factor of 2.4x over QS. In the same line of research we are finalising the porting of QS to GPUs, which, preliminary tests indicate, allows impressive speedups to be achieved.

RapidScorer

AdaQS