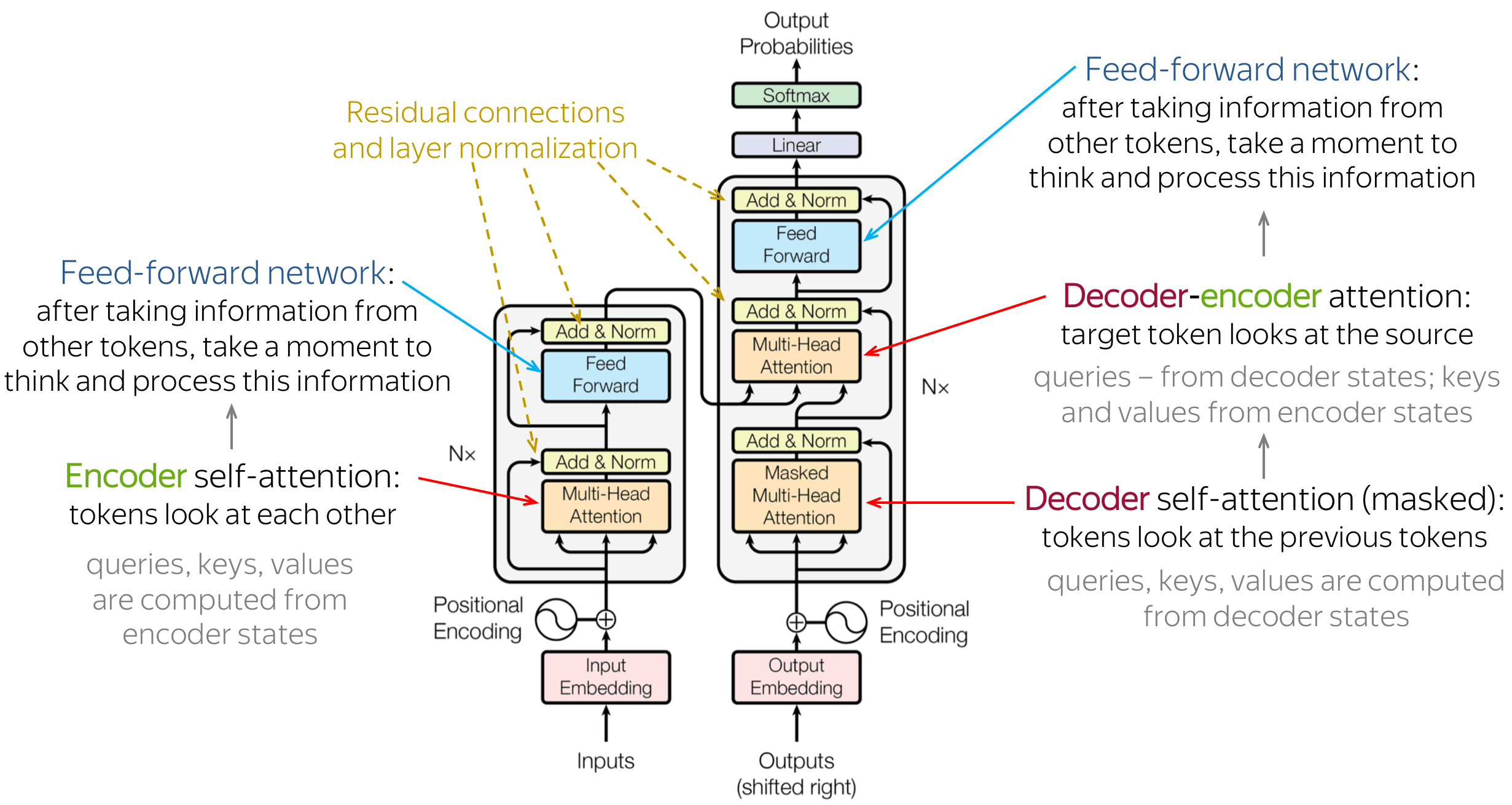
Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence-aligned RNNs or convolution.
Transformer blocks are characterized by a multi-head self-attention mechanism, a position-wise feed-forward network, layer normalization modules and residual connectors.
- The Illustrated Transformer
- The Illustrated BERT, ELMo, and co. (How NLP Cracked Transfer Learning)
- Universal Transformers
- Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View
- The Annotated Transformer
- A Survey of Long-Term Context in Transformers
- The Transformer Family
- https://www.idiap.ch/~katharas/
- https://arxiv.org/abs/1706.03762
- Superbloom: Bloom filter meets Transformer
- Evolution of Representations in the Transformer
- https://www.aclweb.org/anthology/2020.acl-main.385.pdf
- https://math.la.asu.edu/~prhahn/
- https://arxiv.org/pdf/1802.05751.pdf
- https://arxiv.org/pdf/1901.02860.pdf
- Spatial transformer networks
- https://lena-voita.github.io/nlp_course/seq2seq_and_attention.html
- Transformers are graph neural networks
- Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
- A Unified Understanding of Transformer's Attention via the Lens of Kernel
- https://lilianweng.github.io/lil-log/2018/06/24/attention-attention.html
- Attention Is All You Need
- https://arxiv.org/pdf/1811.05544.pdf
- https://arxiv.org/abs/1902.10186
- https://arxiv.org/abs/1906.03731
- https://arxiv.org/abs/1908.04626v1
- 遍地开花的 Attention,你真的懂吗? - 阿里技术的文章 - 知乎
- https://www.jpmorgan.com/jpmpdf/1320748255490.pdf
- Understanding Graph Neural Networks from Graph Signal Denoising Perspectives CODE
- Attention and Augmented Recurrent Neural Networks
- https://www.dl.reviews/
Attention distribution is a probability distribution to describe how much we pay attention into the elements in a sequence for some specific task.
For example, we have a query vector
- https://chulheey.mit.edu/
- https://arxiv.org/abs/2101.11347
- https://linear-transformers.com/
- https://github.com/idiap/fast-transformers
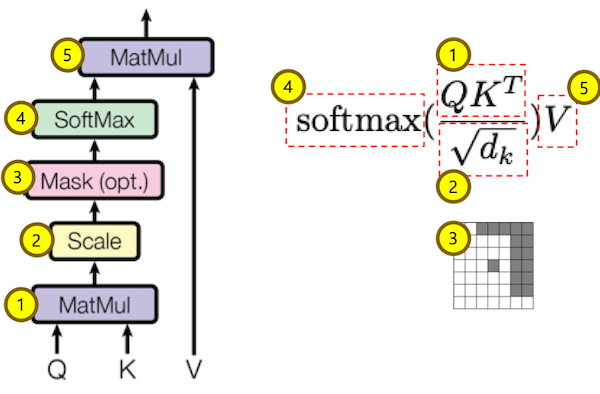
The attention function between different input vectors is calculated as follows:
- Step 1: Compute scores between different input vectors and query vector
$S_N$ ; - Step 2: Translate the scores into probabilities such as
$P = \operatorname{softmax}(S_N)$ ; - Step 3: Obtain the output as aggregation such as the weighted value matrix with
$Z = \mathbb{E}_{z\sim p(\mid \mathbf{X}, \mathbf{q} )}\mathbf{[x]}$ .
There are diverse scoring functions and probability translation function, which will calculate the attention distribution in different ways.
Efficient Attention, Linear Attention apply more efficient methods to generate attention weights.
Key-value Attention Mechanism and Self-Attention use different input sequence as following
$$\operatorname{att}(\mathbf{K, V}, \mathbf{q}) =\sum_{j=1}^N\frac{s(\mathbf{K}_j, q)\mathbf{V}j}{\sum{i=1}^N s(\mathbf{K}_i, q)}$$
where
Each input token in self-attention receives three representations corresponding to the roles it can play:
- query - asking for information;
- key - saying that it has some information;
- value - giving the information.
We compute the dot products of the query with all keys, divide each by square root of key dimension
Soft Attention: the alignment weights are learned and placed “softly” over all patches in the source image; essentially the same type of attention as in Bahdanau et al., 2015. And each output is derived from an attention averaged input.
- Pro: the model is smooth and differentiable.
- Con: expensive when the source input is large.
Hard Attention: only selects one patch of the image to attend to at a time, which attends to exactly one input state for an output.
- Pro: less calculation at the inference time.
- Con: the model is non-differentiable and requires more complicated techniques such as variance reduction or reinforcement learning to train. (Luong, et al., 2015)
Soft Attention Mechanism is to output the weighted sum of vector with differentiable scoring function:
where
In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix
- https://ayplam.github.io/dtca/
- Fast Pedestrian Detection With Attention-Enhanced Multi-Scale RPN and Soft-Cascaded Decision Trees
- DTCA: Decision Tree-based Co-Attention Networks for Explainable Claim Verification
Hard Attention Mechanism is to select most likely vector as the output
$$\operatorname{att}(\mathbf{X}, \mathbf{q}) = \mathbf{x}j$$
where $j=\arg\max{i}\alpha_i$.
It is trained using sampling method or reinforcement learning.
- Effective Approaches to Attention-based Neural Machine Translation
- https://github.com/roeeaharoni/morphological-reinflection
- Surprisingly Easy Hard-Attention for Sequence to Sequence Learning
The softmax mapping is elementwise proportional to
Sparse Attention Mechanism is aimed at generating sparse attention distribution as a trade-off between soft attention and hard attention.
- Generating Long Sequences with Sparse Transformers
- Sparse and Constrained Attention for Neural Machine Translation
- https://github.com/vene/sparse-structured-attention
- https://github.com/lucidrains/sinkhorn-transforme
- http://proceedings.mlr.press/v48/martins16.pdf
- https://openai.com/blog/sparse-transformer/
- Sparse and Continuous Attention Mechanisms
GAT introduces the attention mechanism as a substitute for the statically normalized convolution operation.