Imagine a graph of users and connections between them. User nodes are vertices and the connections between them are edges.
If you wanted to know the number of connections between user A and C, you would have 2 ways of traversing the graph to get your answer:
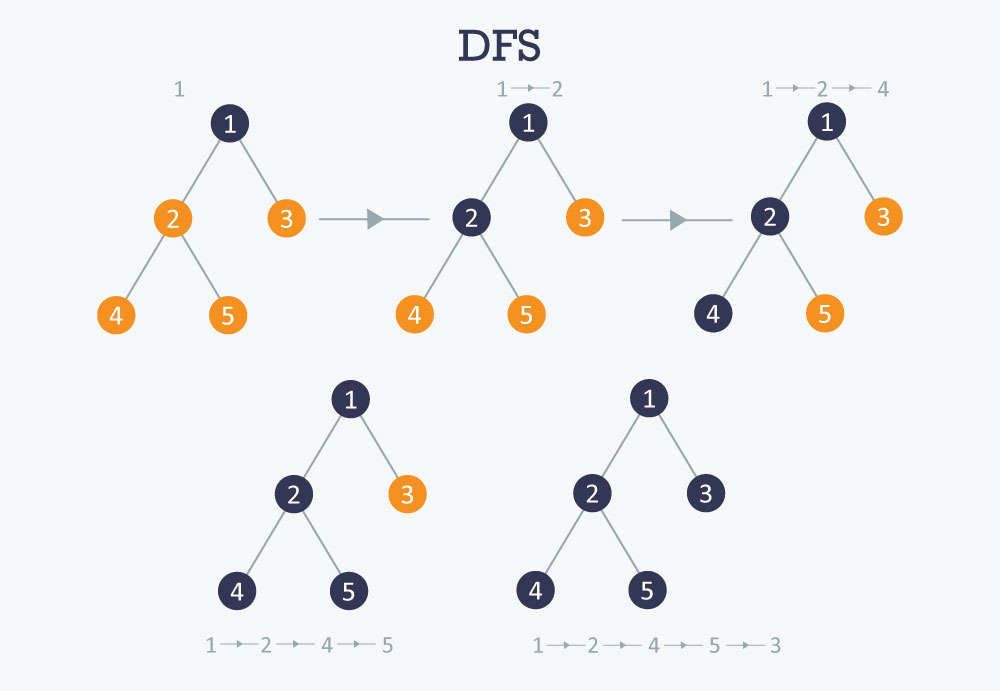
Imagine the graph above where we are trying to count the number of steps between the number 1 and the number 3.
A depth first search algorithm will start from the left and go through the graph like this:
- 1 -> 2
- 2 -> 4
- Back to 2
- 2 -> 5
- Back to 2 -> Back to 1
- 1 -> 3
As this algorithm will keep going through the graph in the current branch until it finds the node it is looking for, it will reach 4 and 5 before it starts looking at the branch on the right and reach 3.
Using this algorithm, a total of 5 nodes are being processed before reaching 3.
A breadth first search algorithm works with layers. It will go through all the nodes on the current layer before going deeper in the graph.
In the graph above, to find the number of steps between 1 and 3, it will do:
- 0 -> 1
- 0 -> 2
- 0 -> 3
It will then process only 4 nodes before reaching 3 from 0. It does not have to go all the way to 4, 5 or 6.
If we take a common graph (below) and try to find the shortest path from the node 8 to 10:
- 8 -> 3 -> 1
- Back to 3
- 6 -> 4
- Back to 6
- 6 -> 7
- Back to 6 -> Back to 3 -> Back to 8
- 8 -> 10
A total of 7 nodes are being processed before the destination is reached.
- 8 -> 3
- 8 -> 10
Only 3 nodes have been processed before reaching the destination.
As a result, BFS is much faster to solve shortest paths problems.