课程中线特征残差是向量形式,面特征残差是标量形式,而作业中需要推导线特征残差的标量形式雅可比和面特征残差的向量形式雅可比。
- 线特征残差
令
则右边第一项为标量对列向量求导,用分子记法的话结果需要转置,为1x3矩阵,可以与第二项直接相乘,最终雅可比为1x6矩阵。
根据李代数相关结论,右边第二项为
- 面特征残差
面特征残差分子为向量的点乘结果为标量,分母也为标量,所以面特征残差取模和不取模是一样的?
class SophusLidarEdgeFactor : public ceres::SizedCostFunction<1, 6> {
public:
SophusLidarEdgeFactor(
Eigen::Vector3d& cur_point,
Eigen::Vector3d& last_point_a,
Eigen::Vector3d& last_point_b) :
cur_point_(cur_point),
last_point_a_(last_point_a),
last_point_b_(last_point_b) {}
virtual ~SophusLidarEdgeFactor() {}
virtual bool Evaluate(double const * const * parameters,
double *residuals, double **jacobians) const {
Eigen::Map<const Eigen::Matrix<double, 6, 1>> lie(parameters[0]);
Sophus::SE3d T = Sophus::SE3d::exp(lie);
Eigen::Vector3d lp = T * cur_point_;
Eigen::Vector3d de = last_point_a_ - last_point_b_;
Eigen::Vector3d nu = (lp - last_point_b_).cross(lp - last_point_a_);
residuals[0] = nu.norm() / de.norm();
if (jacobians != nullptr) {
if (jacobians[0] != nullptr) {
Eigen::Matrix3d lp_hat = Sophus::SO3d::hat(lp);
Eigen::Matrix<double, 3, 6> dp_dse3;
(dp_dse3.block<3, 3>(0, 0)).setIdentity();
dp_dse3.block<3, 3>(0, 3) = -lp_hat;
Eigen::Map<Eigen::Matrix<double, 1, 6>> J_se3(jacobians[0]);
J_se3.setZero();
Eigen::Matrix<double, 1, 3> de_dp =
(nu / (de.norm() * nu.norm())).transpose() * Sophus::SO3d::hat(de);
J_se3.block<1, 6>(0, 0) = de_dp * dp_dse3;
}
}
return true;
}
Eigen::Vector3d cur_point_;
Eigen::Vector3d last_point_a_;
Eigen::Vector3d last_point_b_;
};
class SophusLidarPlaneFactor : public ceres::SizedCostFunction<1, 6> {
public:
SophusLidarPlaneFactor(
Eigen::Vector3d curr_point,
Eigen::Vector3d last_point_j,
Eigen::Vector3d last_point_l,
Eigen::Vector3d last_point_m) :
curr_point_(curr_point),
last_point_j_(last_point_j),
last_point_l_(last_point_l),
last_point_m_(last_point_m) { }
virtual ~SophusLidarPlaneFactor() {}
virtual bool Evaluate(double const *const *parameters,
double *residuals,
double **jacobians) const {
Eigen::Map<const Eigen::Matrix<double, 6, 1>> lie(parameters[0]);
Sophus::SE3d T = Sophus::SE3d::exp(lie);
Eigen::Vector3d lpi = T * curr_point_;
Eigen::Vector3d pipj = lpi - last_point_j_;
Eigen::Vector3d ljm_norm =
(last_point_l_ - last_point_j_).cross(last_point_m_ - last_point_j_);
ljm_norm.normalize();
residuals[0] = pipj.dot(ljm_norm);
// std::cout<<"Residual : "<<residuals[0]<<std::endl;
if (jacobians != nullptr) {
if (jacobians[0] != nullptr) {
Eigen::Matrix3d lp_hat = Sophus::SO3d::hat(lpi);
Eigen::Matrix<double, 3, 6> dp_dse3;
(dp_dse3.block<3, 3>(0, 0)).setIdentity();
dp_dse3.block<3, 3>(0, 3) = -lp_hat;
Eigen::Matrix<double, 1, 6> J = ljm_norm.transpose() * dp_dse3;
jacobians[0][0] = J(0);
jacobians[0][1] = J(1);
jacobians[0][2] = J(2);
jacobians[0][3] = J(3);
jacobians[0][4] = J(4);
jacobians[0][5] = J(5);
}
}
return true;
}
Eigen::Vector3d curr_point_, last_point_j_, last_point_l_, last_point_m_;
};
class PoseSE3Parameterization : public ceres::LocalParameterization {
public:
PoseSE3Parameterization() {}
virtual ~PoseSE3Parameterization() {}
virtual bool Plus(const double *x,
const double *delta,
double *x_plus_delta) const {
Eigen::Map<const Eigen::Matrix<double, 6, 1>> lie(x);
Eigen::Map<const Eigen::Matrix<double, 6, 1>> delta_lie(delta);
Sophus::SE3d T = Sophus::SE3d::exp(lie);
Sophus::SE3d delta_T = Sophus::SE3d::exp(delta_lie);
Eigen::Matrix<double, 6, 1> x_plus_delta_lie = (delta_T * T).log();
for (size_t i = 0; i < 6; i++) {
x_plus_delta[i] = x_plus_delta_lie(i, 0);
}
return true;
}
virtual bool ComputeJacobian(const double *x, double *jacobian) const {
ceres::MatrixRef(jacobian, 6, 6) = ceres::Matrix::Identity(6, 6);
return true;
}
virtual int GlobalSize() const {return Sophus::SE3d::DoF;}
virtual int LocalSize() const {return Sophus::SE3d::DoF;}
};// 添加线特征残差
ceres::CostFunction *cost_function =
new SophusLidarEdgeFactor(curr_point, last_point_a, last_point_b);
problem.AddResidualBlock(cost_function, loss_function, sophus_param);
// 添加面特征残差
ceres::CostFunction *cost_function =
new SophusLidarPlaneFactor(curr_point, last_point_a, last_point_b, last_point_c);
problem.AddResidualBlock(cost_function, loss_function, sophus_param);
// 添加参数块
double sophus_param[6];
Sophus::SE3d pose_se3(q_last_curr, t_last_curr);
Eigen::Matrix<double, 6, 1> pose_vec = pose_se3.log();
sophus_param[0] = pose_vec(0, 0);
sophus_param[1] = pose_vec(1, 0);
sophus_param[2] = pose_vec(2, 0);
sophus_param[3] = pose_vec(3, 0);
sophus_param[4] = pose_vec(4, 0);
sophus_param[5] = pose_vec(5, 0);
problem.SetParameterization(sophus_param, new PoseSE3Parameterization());
// update SE3
Eigen::Matrix<double, 6, 1> vec;
vec(0, 0) = sophus_param[0];
vec(1, 0) = sophus_param[1];
vec(2, 0) = sophus_param[2];
vec(3, 0) = sophus_param[3];
vec(4, 0) = sophus_param[4];
vec(5, 0) = sophus_param[5];
Eigen::Matrix4d T = Sophus::SE3d::exp(vec).matrix();
t_last_curr.x() = T(0, 3);
t_last_curr.y() = T(1, 3);
t_last_curr.z() = T(2, 3);
Eigen::Quaterniond q(T.block<3, 3>(0, 0));
q_last_curr.w() = q.w();
q_last_curr.x() = q.x();
q_last_curr.y() = q.y();
q_last_curr.z() = q.z();- A-LOAM自动求导
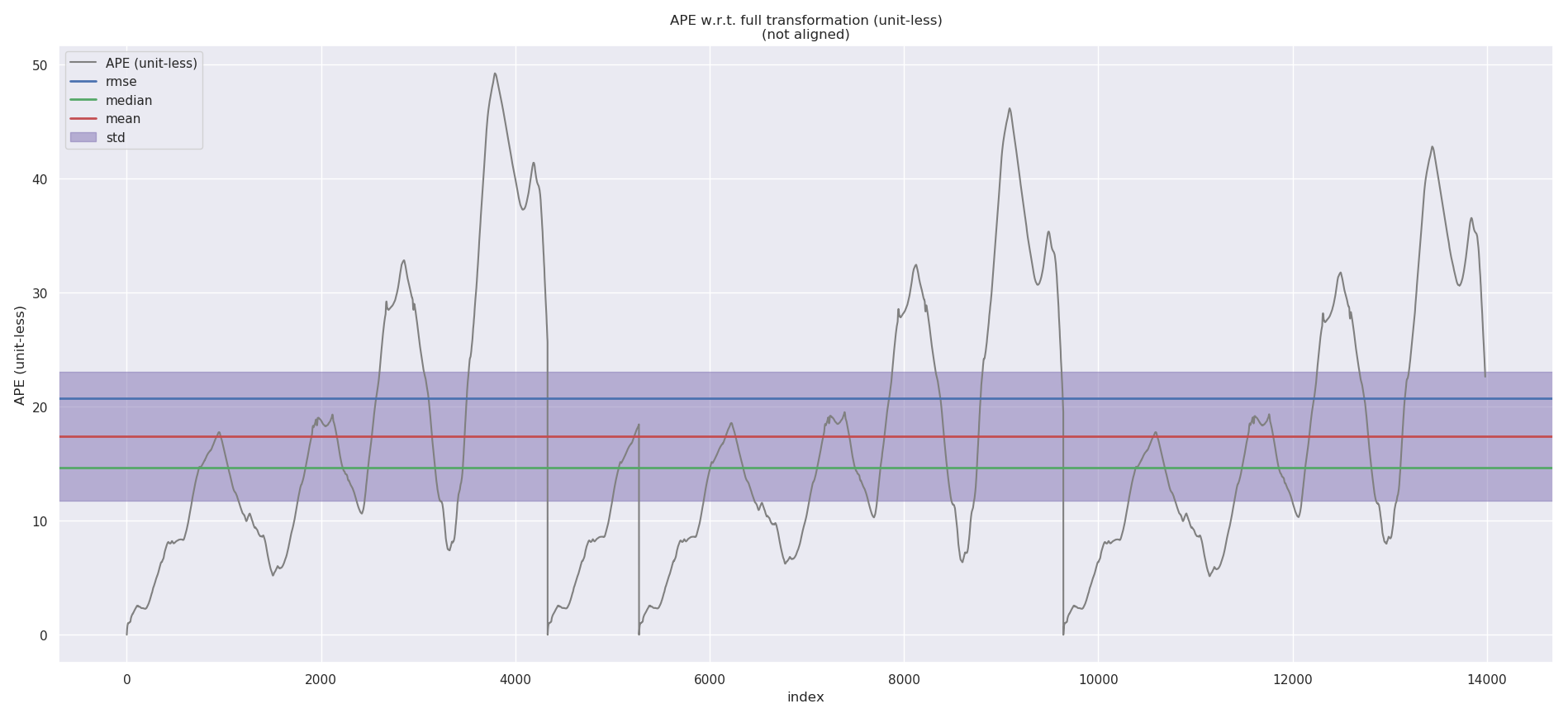
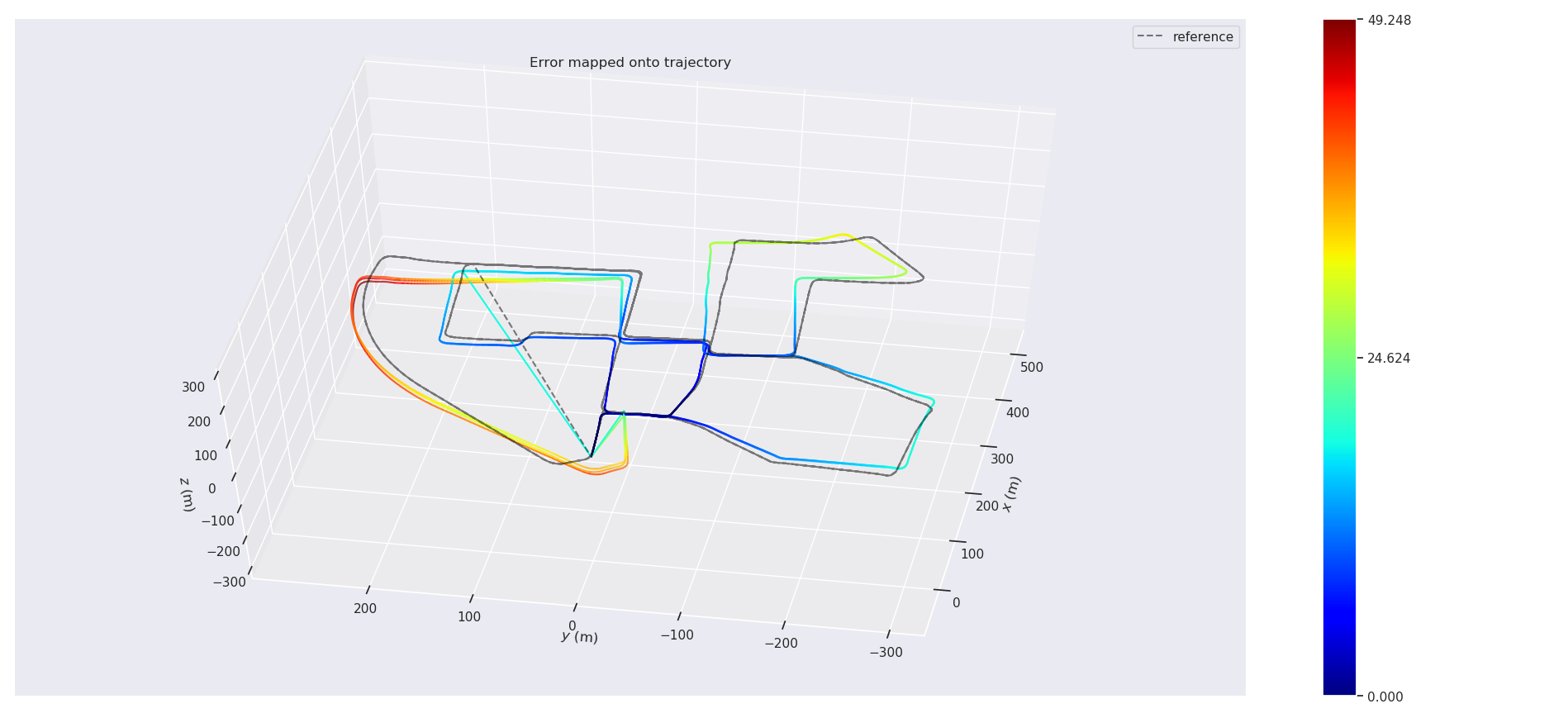
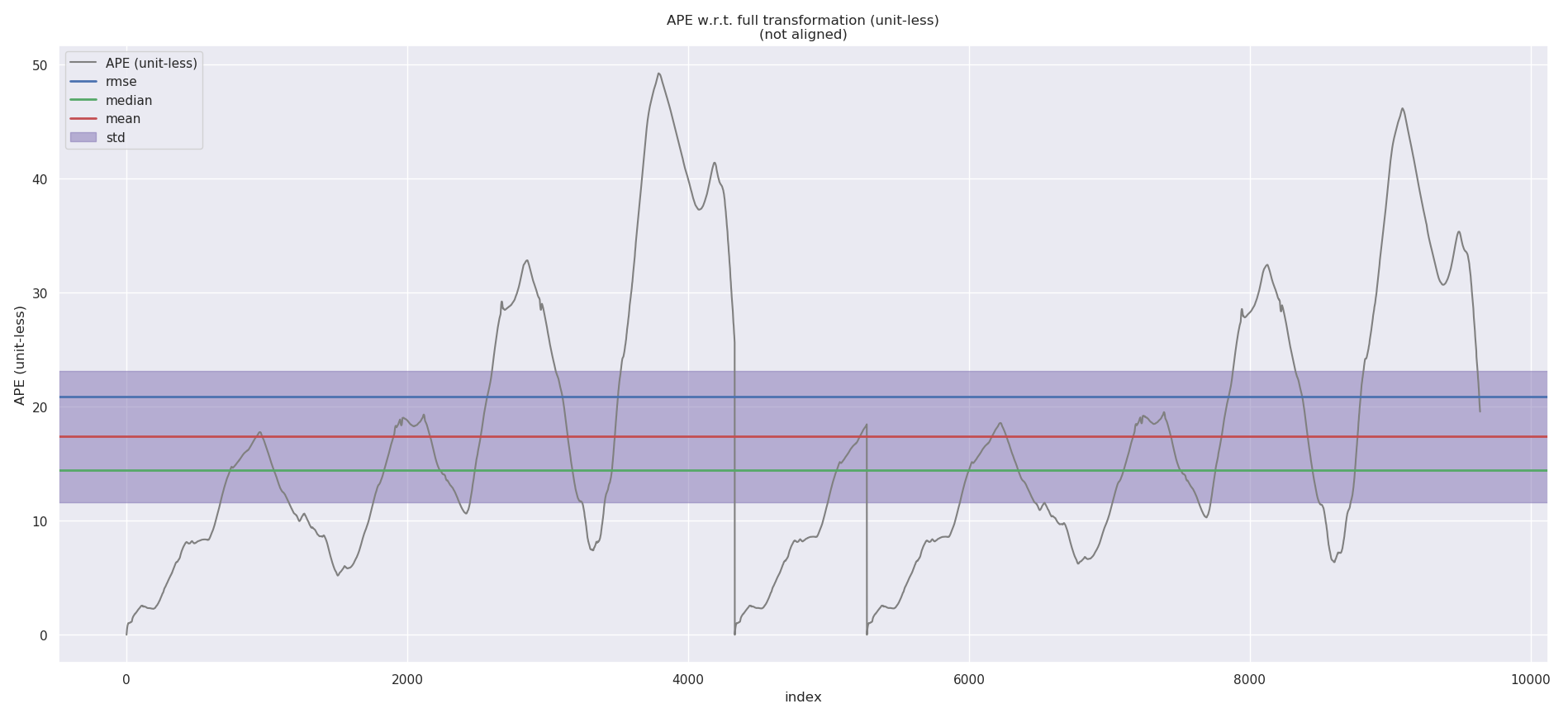
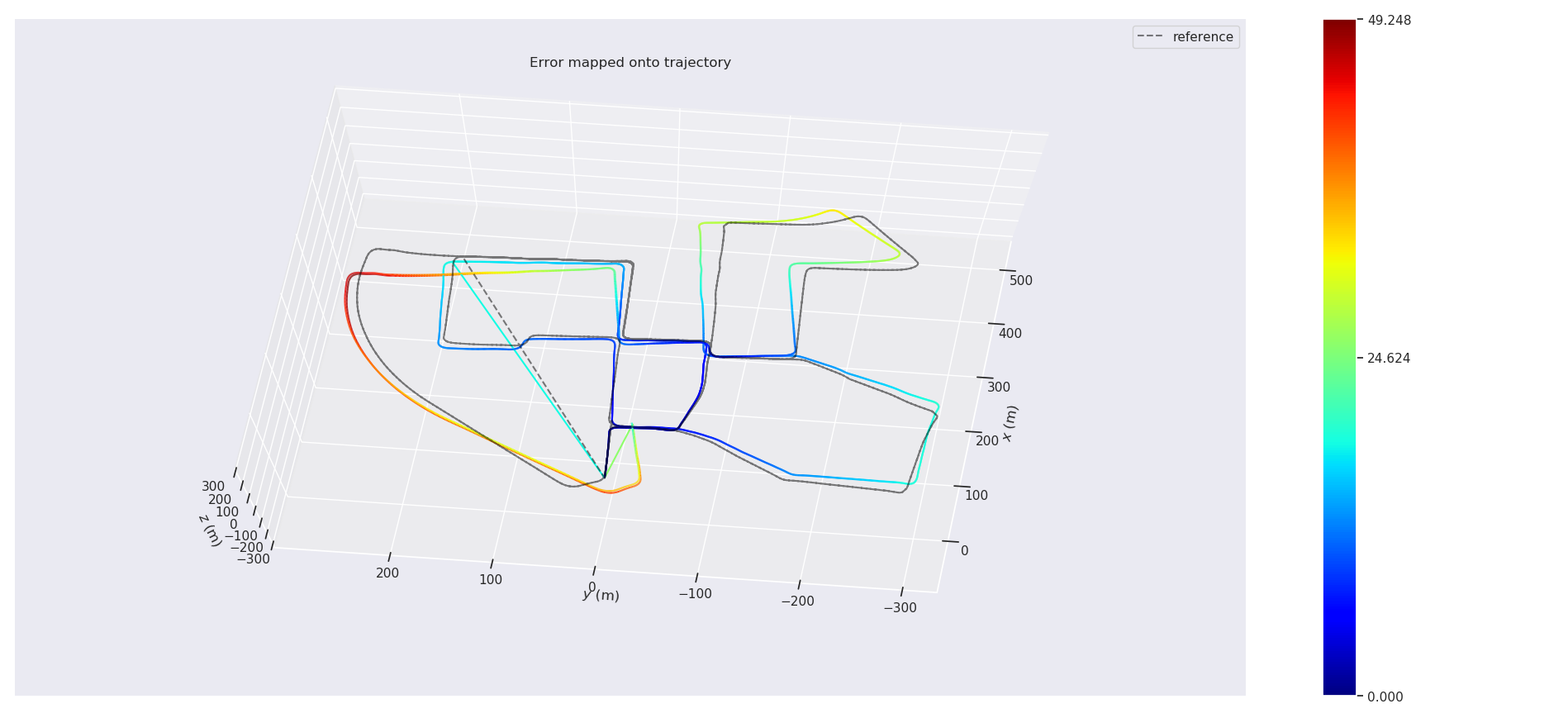
APE w.r.t. full transformation (unit-less)
(not aligned)
max 49.247754
mean 17.414580
median 14.640529
min 0.000000
rmse 20.736299
sse 6013037.677376
std 11.257287
- A-LOAM解析求导
APE w.r.t. full transformation (unit-less)
(not aligned)
max 49.247754
mean 17.377848
median 14.454931
min 0.000000
rmse 20.878923
sse 4202795.712532
std 11.573238
对比发现解析求导和自动求导效果非常接近。