EMorav
This program can be used to compute the average orientation for a list of orientations in arbitrary representation. The program uses four different appraches to orientation averaging:
- quaternion averaging using the quaternion logarithm
- quaternion averaging using the T-matrix eigenvalue approach
- von Mises-Fisher (VMF) distribution fit of mean orientation and concentration
- Watson (WAT) distribution fit of mean orientation and concentration
Each of these produces the mean quaternion, and they all work correctly in the absence of rotational symmetry. When a fundamental zone is applied to the input rotations, then it is very likely that the first two approaches will not provide the correct average orientation because these algorithms do not take crystal symmetry into account. In the case of the VMF/WAT approaches, known as directional statistics approaches, the rotational symmetry is properly taken into account. The details of these algorithms are described in the following papers:
- Y.H. Chen, Park S.U., D. Wei, G. Newstadt, M. Jackson, J.P. Simmons, M. De Graef, and A.O. Hero. “A selfionary approach to the EBSD indexing problem”. Microsc. MicroAnal. 21, 739-752 (2015).
- Y.H. Chen, D. Wei, G. Newstadt, M. De Graef, J.P. Simmons, and A.O. Hero. “Parameter estimation in spherical symmetry groups”. IEEE. Sign. Proc. Lett. 22, 1152-1155 (2015).
In each case, the algorithm produces the mean orientation and a parameter known as the concentration, which is a measure for the full-width-at-half-maximum of the isotropic von Mises-Fisher and Watson distributions. The main difference between the two distributions is that the Watson distribution takes into account the fact that the quaternions q and -q represent the same orientation.
The program uses the standard name list approach and the name list template file can be obtained with the -t command line option; rename the file to EMorav.nml.
&orav
! point group number; please use 0 if no symmetry reduction should be applied
! #1: '1', #2: '-1', #3: '2', #4: 'm', #5: '2/m', #6: '222', #7: 'mm2', #8: 'mmm'
! #9: '4', #10: '-4', #11: '4/m', #12: '422', #13: '4mm', #14: '-42m', #15: '4/mmm', #16: '3'
! #17: '-3', #18: '32', #19: '3m', #20: '-3m', #21: '6', #22: '-6', #23: '6/m', #24: '622'
! #25: '6mm', #26: '-6m2', #27: '6/mmm', #28: '23', #29: 'm3', #30: '432', #31: '-43m', #32: 'm-3m'
pgnum = 32,
! relative path to the orientations file [relative to EMdatapathname]
orientationfilename = 'undefined',
/There are only two parameters: the name of the orientation input file, and the point group symmetry to be applied to the orientations. A point group number of 0 means that no fundamental zone symmetry reduction should be applied.
The input orientations file should have the standard EMsoft format for orientation files: on the first line of the text file the orientationm representation is identified using a two character abbreviation from the list
- ro = Rodrigues vector
- qu = quaternion
- ho = homochoric vector
- st = 3D stereographic vector
- ax = axis angle pair
- om = orientation matrix
- rv = rotation vector
- cu = cubochoric vector
The second line contains the number of orientations in the remainder of the file; this number can be set to a value smaller than the actual number present in the file. Next are the orientations in the correct format, one per line; one can use spaces or commas to separate the values/components.
The program is then executed by calling it from the command line with the name list file name as single argument. All program output is sent to the terminal window.
Let's consider a simple example: a uniformly sampled set of orientations that all have a maximum misorientation of 7° with respect to the rotation 45°@[100] [corresponding to (0.9238795,-0.3826834,0,0) in quaternion form; note that the minus sign can also be a plus sign since the two are equivalent orientations]. One can use misorientation sampling mode of the EMsampleRFZ program to generate this orientation set; see the manual page for this program for details. For a value of N=15, the program generates a data set of 29,791 orientations in quaternion format.
qu
29791
0.908668101 0.414533070 0.046051629 0.019075209
0.908305347 0.415408835 0.046170917 0.016886159
0.907960635 0.416241043 0.046219656 0.014649985
0.907635280 0.417026521 0.046195754 0.012370613
0.907330559 0.417762182 0.046097364 0.010052315
0.907047704 0.418445054 0.045922911 0.007699694
0.906787887 0.419072309 0.045671117 0.005317663
0.906552208 0.419641286 0.045341015 0.002911417
...Running EMorav with point group number set to 0, the output is:
Number of orientations read : 29791
Quaternion logarithmic average [CAUTION]
<q> 0.92396079846033119 0.38248718005777305 -2.7238198760463652E-020 -1.3959576864737621E-020
st. dev. 0.99876638781298688 2.8174930189429803E-002 2.8912591407715973E-002 2.8912591407715973E-002
-----------
Quaternion T-matrix average [CAUTION]
<q> 1.0000000000000000 0.0000000000000000 0.0000000000000000 0.0000000000000000
st. dev. 3.4398699292744747E+034 159103632.00000000 -159103632.00000000 2.6017421856522560E-002
-----------
Quaternion von Mises-Fisher average
<q> 0.92387953253637822 0.38268343230451357 -4.5706608079224806E-020 6.8793109098833276E-020
kappa 1258.7018807840063
eq. deg. 2.2840465282609310
-----------
Quaternion Watson average
<q> 0.92387953253638455 0.38268343230449831 -3.7313242220614706E-016 0.0000000000000000
kappa 630.48497368191408
eq. deg. 3.2274362963926690 All but the T-matrix approach return the correct answer. When the point group is set to 32 (cubic), then the output becomes:
Number of orientations read : 29791
Quaternion logarithmic average [CAUTION]
<q> 0.99991987414810990 1.2658802614308616E-002 2.4781933884171215E-019 -2.0764186144491200E-019
st. dev. 0.93188683050838195 0.36055160402573910 2.8191097526603721E-002 2.8191097526603731E-002
-----------
Quaternion T-matrix average [CAUTION]
<q> 1.0000000000000000 0.0000000000000000 0.0000000000000000 0.0000000000000000
st. dev. 0.0000000000000000 0.0000000000000000 -1.8191415540503074E+030 0.0000000000000000
-----------
Quaternion von Mises-Fisher average
<q> 0.92387953248619703 -0.38268343242566172 2.4042608637592346E-019 2.2666746455615673E-019
kappa 1258.7018807789618
eq. deg. 2.2840465282653999
-----------
Quaternion Watson average
<q> 0.92387953248618859 -0.38268343242568215 -2.5231975340965170E-016 0.0000000000000000
kappa 630.48497367932964
eq. deg. 3.2274362963993348 Both quaternion averages return essentially the identity orientation, whereas the directional statistics algorithms produce the correct results for both VMF and WAT. Note that it is possible that the routines return one of the symmetrically equivalent orientations; this is often due to rounding issues when determining which point lies inside the FZ, when the average lies close to or on the FZ boundary.
The value of the concentration parameter, kappa, can be converted into an equivalent angle; this is related to the FWHM of the VMF/WAT distributions.
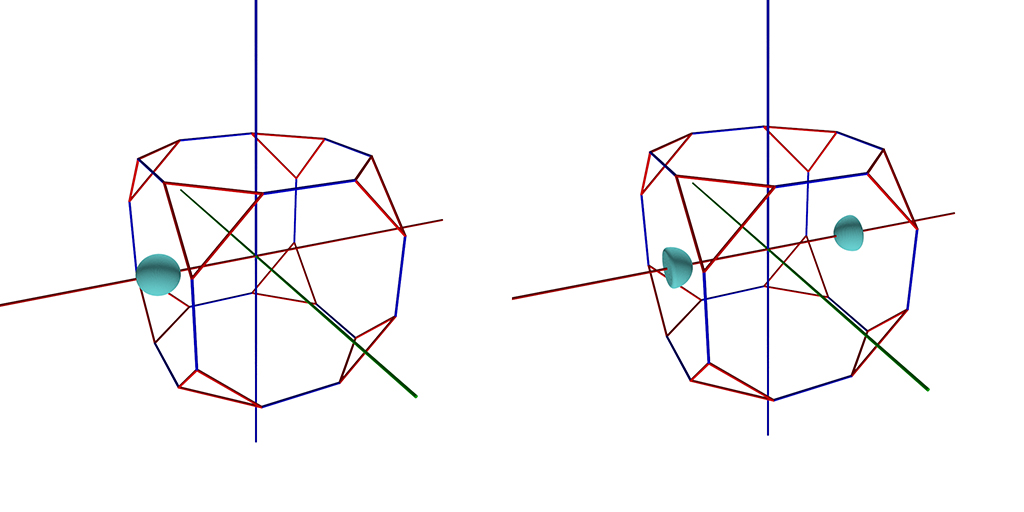
The Rodrigues space figures below illustrate what happens in this example; on the left, the cubic FZ is shown along with an ellipsoid (nearly a sphere) depicting the set of orientations at 7° misorientation from the rotation 45°@[100]. On the right, cubic symmetry is applied to the orientations, so that half of the ellipsoid moves towards the opposite side of the FZ. The quaternion averaging routines do not take symmetry into account, so the average between the two semi-ellipsoids ends up in the middle of the FZ at the identity rotation. For the VMF/WAT algorithms, cubic symmetry is applied on the quaternion hemisphere before the mean orientation is determined, so the result does not suffer from the presence of the FZ boundaries.
