-
Notifications
You must be signed in to change notification settings - Fork 26
supertrees using tree ranking
As of 26-Feb-2015 some of us (MTH and EJM) are pursuing supertrees via "ranked trees on a taxonomic scaffold" as a strategy.
The overall goal of the project is to summarize what is known about phylogenetic relationships in a transparent manner with a clear connection to analyses and the published studies that support different clades. Comprehensive coverage of published phylogenetic statements is a very long term goal which would require work from a large community of biologists. The short-term goal for the supertree presented on the tree browser is to summarize a small set of well-curated inputs in a clear manner.
We hope that this tree (and its many deficiencies) will inspire biologists to help fix the tree by alerting us to relevant phylogenetic statements that are missing in our set of inputs or contributing to the Open Tree effort in other ways. We have built tools to support 2 types of feedback:
- Our phylogenetic study curator tool for adding new input trees.
- Clade-linked issue reports. Click on "See comments" on a node of the tree, such as the Tetrapoda node to see a conversation that is tied to a particular phylogenetic grouping. Full issue-tracking features for that conversation (e.g. notifications, authenticated comments, tagging, closing of the issue) are supported using GitHub issues system. This issue on GitHub contains the thread about the groupings shown at the Tetrapoda node linked above.
Of course, emailing comments is another way to provide feedback (see the opentreeofliife group for general comments and this list for software issues).
Note: MTH put together this list. #3 may not be agreed upon by all participants.
- produce a full supertree: The set of taxa associated with leaves of the supertree is the set of "terminals" in the taxonomic input.
- the tree should display (in the sense described here) as many edges from the curated input trees as possible . If the scoring criterion was a count of the number of groupings, then this would surely by an NP-hard problem REF needed. 1. ranked trees property: For simplicity of implementation, we use a tree-based ranking system to resolve conflicts for simplicity. 2. taxonomy last property: the taxonomy is the lowest ranked input
- Display no unsupported groupings sensu the definition describe in this doc.
- this one definitely needs some work: we might want some statement about the placement of groups that appear in only one source tree. Perhaps: when there is a large set of attachment points to which a group can be attached and still display the same set of input tree edges, then the group should be attached at the point closest to the root that is consistent with these displayed set. This placement is in the spirit of the Adams consensus (see this nice write up by Rod Page; for a more mathematical discussion, see this excellent review by David Bryant) of all of the attachment points.
- the tips of all input trees have been mapped to a common taxonomy (a pruned version of OTT in our case),
- if more than one species maps to the same OTT ID, then the tree has been pruned until this is not the case.
- if a tip maps to a higher taxon in OTT and another tip in the tree maps to taxon within the higher taxon, then one of the tips has been pruned (process repeated until the condition no longer applies).
- labels of internal nodes in the input phylogeny are ignored by the supertree algorithm.
- any redundant nodes (nodes of out-degree=1) have been suppressed.
- all trees are rooted.
The taxonomic input is a pruned version of OTT created by reading in OTT (2.8) and pruning taxa that have certain flags Needs documentation!
One very important processing step that treemachine does is remapping a tip in a tree to the deepest taxon that it could be considered to exemplify. MTH does not know if this step is discussed in any publication.
Operationally, this step consists of finding the deepest node in the taxonomy that is an ancestor of the tip's taxonomic label, but which is not an ancestor of any taxa that are the "outgroup" of that leaf with respect to the input tree.
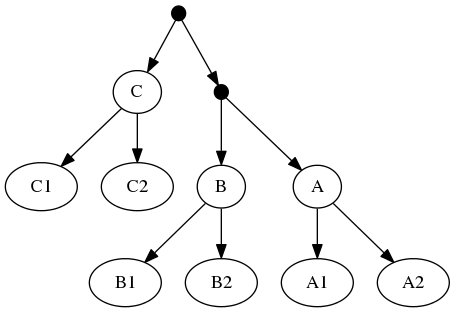
To understand why this is important, consider the following inputs:
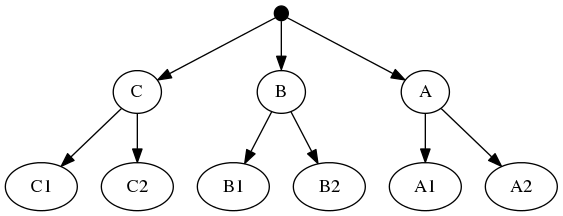
The highest ranked tree: 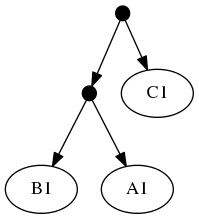
And the taxonomic tree:
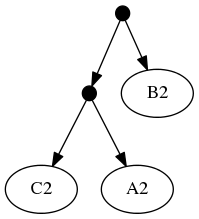
Note that the phylogenetic inputs have no overlap in their leaf sets. Thus, directly applyting the tree ranking score criterion (called WSITED on this page) to these inputs would return the following "phylo-only" tree.
phylo-only solution:
That solution displays both of the groups from the input phylogenies, but lacks any of the 3 higher level taxa from the taxonomic input.
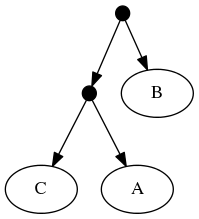
Because of the treemachine remapping to the deepest exemplified taxon. To do this, we note that A1 (in the first tree is the only representative of group A in that tree. Thus, we could view the leaf that a curator has mapped to taxon A1 as (narrowly) merely making a statement about that species. Or we could view it as making a statement about the entire group A. Moving one further node back in the taxonomy would reach a taxon A+B+C; this taxon is represented multiple times in tree 1 (by different tips). Thus, the deepest taxon that uniquely maps to A1 is the group A; treemachine would interpret the input tree as if it were mapped to A. This procedure would preprocess the inputs to:
The highest ranked tree: 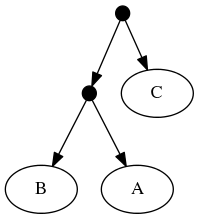
When viewed in terms of the deep taxon exemplified, the first and second tree are now seen as in conflict. Using the tree ranking, the former is preferred. This leads to a "skeleton" of the phylogeny that looks like tree 1. Onto that backbone, the taxonomy can fill out the tip labels. Thus the "tip-as-deepest-taxon-exemplar solution" is:
Frustratingly, it is probably not the case that one of these strategies is always best. Treemachine's "tip-as-taxon-exemplar" approach allows many more trees to make overlapping statements, so it leads to correctly highlighting the conflict in many cases.
Imagine that A1 and A2 were the chimps Pan troglodytes and Pan bonobo respectively; B1 and B2 were two species in the genus Equus (horses); and C1 and C2 were two lemmings (cute little things in the genus Lemmus). If that were the case, then the taxonomy would have many more level in this case, but the deepest-taxon-exemplified by the leaves would be something like Primates, Perissodactyla, and Rodentia. It is highly unlikely that the taxonomic understanding of the tips is so wrong that these deeper groups are not monophyletic with respect to these tips. Clearly this would be a case of two phylogenies conflicting with respect to the relationships between Primates, Rodents, and Perissodactyls. The "phylo-only" solution would imply that Pan troglodytes is more closely related one of the Equus species than it is to Pan bonobo. Which is just silly.
However, if the phylo-only solution is an appealing one if the tips are all closely related species in some poorly studied taxon with lots of "wastebin" groups. For example, if all 6 species were in the notoriously difficult Lygosominae group of skinks, then we might be much happier to believe that the phylo-only solution is a better statement of what we know. Based on the phylogenetic estimates, we can make some statements about the species that have been sampled in a phylogeny. All other members of these problematic "taxa" probably should simply be attatched as a polytomy at the base of the phylo-only solution. The phylo-only solution reveals the fact that A, B, and C are not monophyletic taxa; so we need more phyloegenetic estimates that cover these species.
One could imagine counting the intervening number of higher taxa to decide which of these approaches should be used. That could lead to some easy rule like "you can remap back some number, X, levels in the taxonomy, but no more." So this would be a deeper taxon rule. This sounds arbitrary, too sensitive to the taxonomic input, and not terribly transparent (unless you are staring at the taxonomic tree when interpreting the synthetic tree) to MTH. So (as of the initial writing on 9-Feb-2015) this does not seem worth pursuing.
This would entail:
- reading in the taxonomy,
- reading in each of the input trees (with no remapping of leaves to deeper taxa)
- flagging an each taxon for which there is some conflict (at least one tree disagrees with the monophyly of the group). Mark these taxonomic nodes as "contested taxa"
- reprocessing the tips of the input trees and remapping each leaf by moving to higher taxon that the leaf could exemplify (as treemachine does), but with the modification that the remapping stops at a taxon if the parent of the taxon is a "contested taxon".
Note that this would not have any special abilities to force the mapping into the preferred interpretation of taxonomic labels. Getting that right on a consistent basis seems to involve some biological knowledge about the trustworthiness of the taxonomy.
If the tips in the example above were from wastebin groups, then this proposal would not detect the problem. In the inputs above there is no evidence of non-monophyly of A, B, or C in any single input tree (the evidence of non monophyly is in the phylo-only solution). So in the example above, the "remap tips to deepest uncontested taxon" approach would be the same as the "remap tips to deepest taxon."
On the positive side, adopting the "remap tips to deepest uncontested taxon" approach to supertrees would mean that any cases of the taxonomy of wastebin groups being taken to seriously has an obvious, data curation response: "Someone, please add a tree that provides evidence for the non-monophyly of the taxa". If someone added such a tree, then the next run of the supertree algorithm will see the conflict, and would treat the input labels of these 2 trees differently - they would stay tied to taxa closer to the species names that the study curator mapped the tips to.
Note that the tips of the input trees need not be mapped to a terminal taxon in the pruned OTT.
The interpretation of such tips is not always clear. We assume the following of a tree, t, that has a tip mapped to a higher taxon Y:
- The presence of a
Yas a tip intshould not be taken as evidence of the monophyly of the taxon. - If building the supertree with all of the inputs except for the fact that
Yis pruned fromtreturns a supertree in whichYis monophyletic, then we say that the analysis supports the monophyly ofY. Note that, in many cases, this might be easy to check by performing small scale synthesis only trees that support or reject the monophyly ofY. - If the analysis without
Yintsupports the monophyly ofY, then replacingYwith a polytomy of all of the contained tips underYconveys the same phylogenetic information astwith the exception of the fact that the "taxonomically expansion" appears to provide support for monophyly. - If the analysis without
Yintrejects the monophyly ofY, then the input tree withYas a tip label is difficult to interpret. We assume in these cases, it is acceptable to pruneYoff of treetbecause that information fromtabout this group of species is ambiguous.
We will consider adopting a more aggressive form of pruning to avoid ambiguous inputs: if any of the phyloenetic trees reject the monophyly of the taxon Y, then we will prune Y from t. In other words, if (based on the trees other than t), Y is a "contested taxon", then we will prune Y when processing t. This decision is convenient, but also justifiable because the algorithm has detected that there is some controversy about the meaning of the input.
If no tree rejects the monophyly of the taxon, then the taxonomy will support its monophyly. So the lack of reject of monophyly by a phylogenetic input implies support for monophyly from the full analysis (which includes the taxonomic tree).
If a tip is mapped to a non-leaf taxon, and it is not pruned, then it will be subjected to the "remap to deepest uncontested taxon" rule described as preprocessing step 1.
The strong preference for grouping based on tree-ranking simplifies the supertree construction problem considerably.
Conjecture 1: The set of equally optimal trees (A) can be expressed as a forest of rooted phylogenetic networks, but (B) may not necessarily be expressable as a tree.
Note: Retained for the sake of posterity, but part (A) conjecture is false. See https://github.com/OpenTreeOfLife/opentree/wiki/phylogenetic-graphs for discussion of the counter example. Also note that the modified statement is "The set of equally optimal trees (A) can be expressed as a set of graphs each of which is a forest of rooted phylogenetic networks, but..."
We will use the phrase "phylogenetic graph" to refer to a direct graph in which each connected component in which each connected component is a phylogenetic network (contains no directed cycles).
One can think of an incompletely resolved tree (a tree with polytomies) as representing the set of trees that can be obtained by fully resolving the polytomies (but retaining all groupings in the original trees).
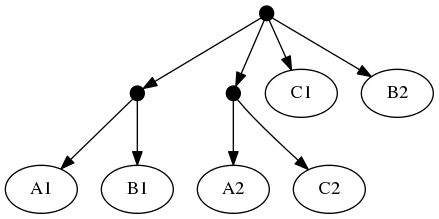
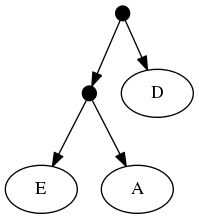
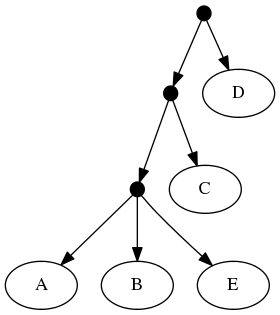
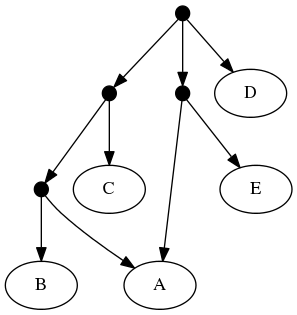
The proof of (B) is straightforward. Consider the inputs:
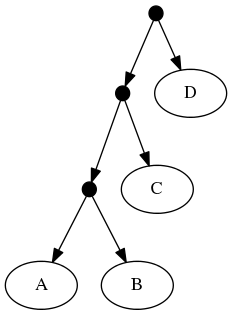
The follwing set of trees that can be produced by taking the union of all resolutions of both of these trees:
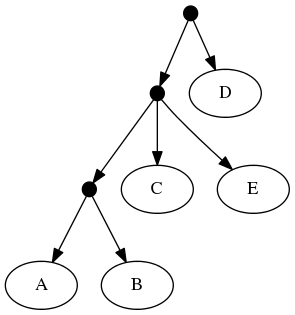
Or by the phylogenetic network:
But not by the set of all trees that resolve the:
or any other tree because no tree displaying the rooted triplet ((A,C),B) is a valid solution.
We hope to prove part (A) of the conjecture by describing an algorithm.
Retained for the sake of posterity, but part (A) conjecture is false. See https://github.com/OpenTreeOfLife/opentree/wiki/phylogenetic-graphs
Consider the case of an clade or single tip referred to as X is present in an input tree, t, but:
- no taxa assigned to
Xa have been added to a directed phylogengetic network,N, and -
Nhas all of the other taxa from inta connected component. - the edge that connects
Xto the rest oftis not a edge adjacent to a root with out-degree=2.
The procedure that we will call "phyloreference placement" of X consists of:
- generating a phylogenetic definition of the node or edge that
Xattaches to intwhich uses as designators all of the relevant leaf taxatexcept the taxa underX. This could be the definition of an edge (if the parent ofXis bifurcating, or a node if the parent ofXis a polytomy). In the case of a node definition the phyloreference is a statement of all of the taxa that descend from the node. For an edge definition, the descendant taxa of the edge and the "outgroup" are all included in the definition. - looking for a corresponding edge, path, or node in
Nbased on the definition: 1. if an edge is found,Xis added to theNcreating a parent for it that bisects the edge; 2. if a node is found, then it is treated as the parent toX3. if a path is found, thenXis attached by creating a loop from the start node of the path to the end node and and adding a parent forXalong that path. 4. if the object defined by the phyloreference forXdoes not exist, then the descendant leaf set of the grandparent ofXis calculated. The LICA of these leaves inNwill serve as the parent of theXwhen it is attached to the graph.
Conjecture 2: The procedure "prune off singletons, infer the graph, then use 'phylogenetic placement' to add the singletons" finds the optimal solution.
If there exists a node X in one input trees, t such that all of the leaves correspond to taxa which are not found in any of the of the input trees other than t, then we call the group defined by X a "single-source clade" or a "singleton."
If we were to find the phylogenetic graph that represents the optimal solution it would be identical to the solution that one could obtain by:
- pruning the single-source clade from the input tree,
- finding the optimal phylogenetic graph for the pruned inputs,
- using phyloreferencing placement to attach
Xto the graph.
Conjecture 3: Building the phylogenetic graph by adding one tree at a time (in rank order) produces the optimal solution.
Because of the strong preference for groupings from trees of high importance, the algorithm does not need to consider the downstream consequences of adding a split. A greedy approach works because the addition of weight to the score from satisfying one edge from a high importance tree is larger than the score benefit from adding all of the groupings from trees of lower importance.
note conjecture 4: should also demonstrate that the order that you try to add groups from within the same tree does not have side effects - in the sense that any order of additions of groups from a tree to a network will result in the same output. This seems intuitive because all of the groupings within the same tree are compatible. But I am not certain if it holds, given that we are adding to phylogenetic network (rather than a tree).
NOTE (MTH 26-Feb) turns out that conjecture 4 is not true. The A, B, C example discussed above in "The tip-as-deepest-taxon-exemplar approach" is a counter example. END NOTE
See this page for one discussion of a scoring criterion which MTH thinks could be viewed as a criterion that the automated "tree synthesis" attempts to solve. This page will discuss some algorithmic considerations about this style of synthesis.